浩瀚宇宙 灿烂星空

工作和生活中的七七八八

0%

发表于 更新于 分类于 ， 阅读次数： Disqus： Valine：

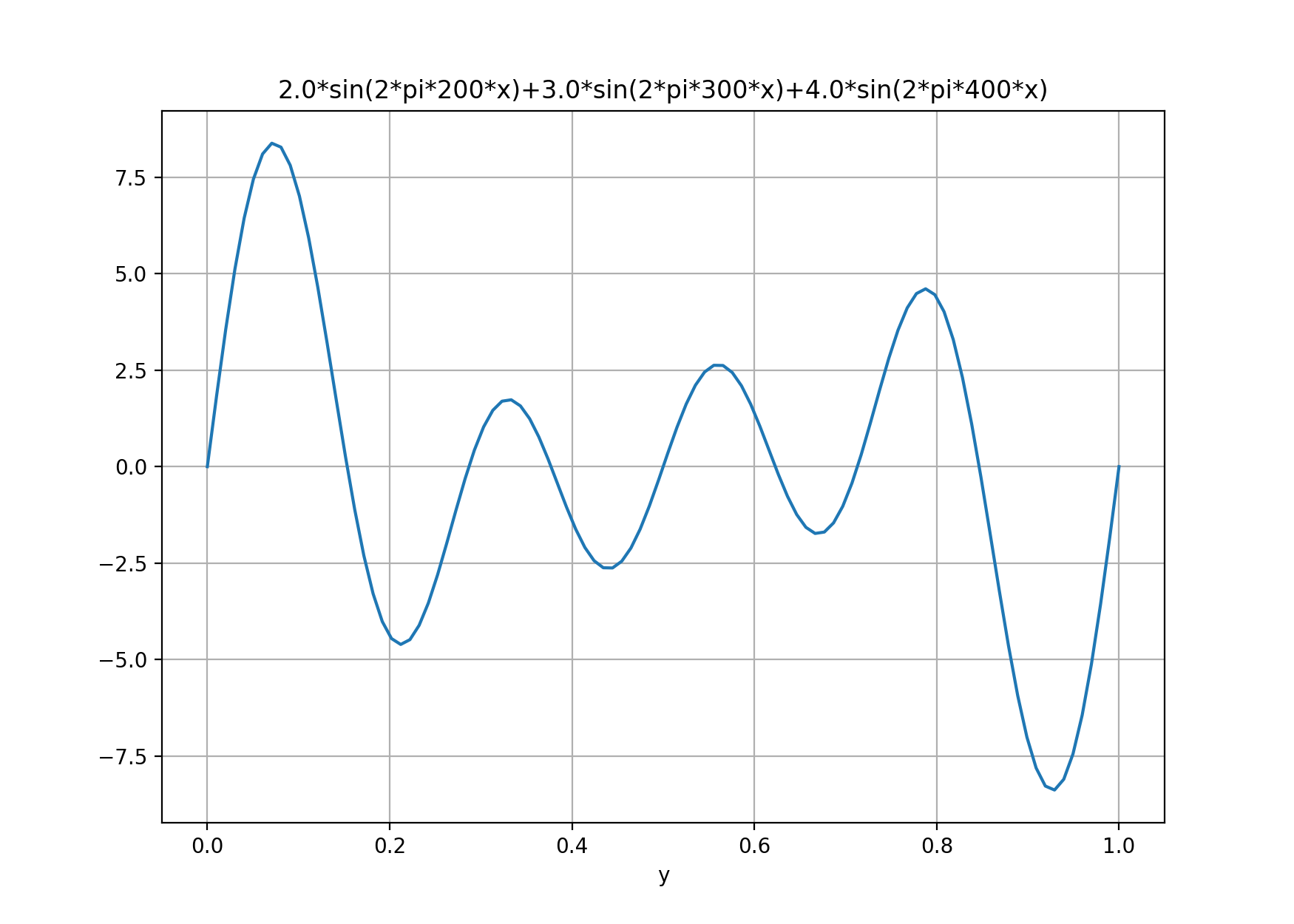
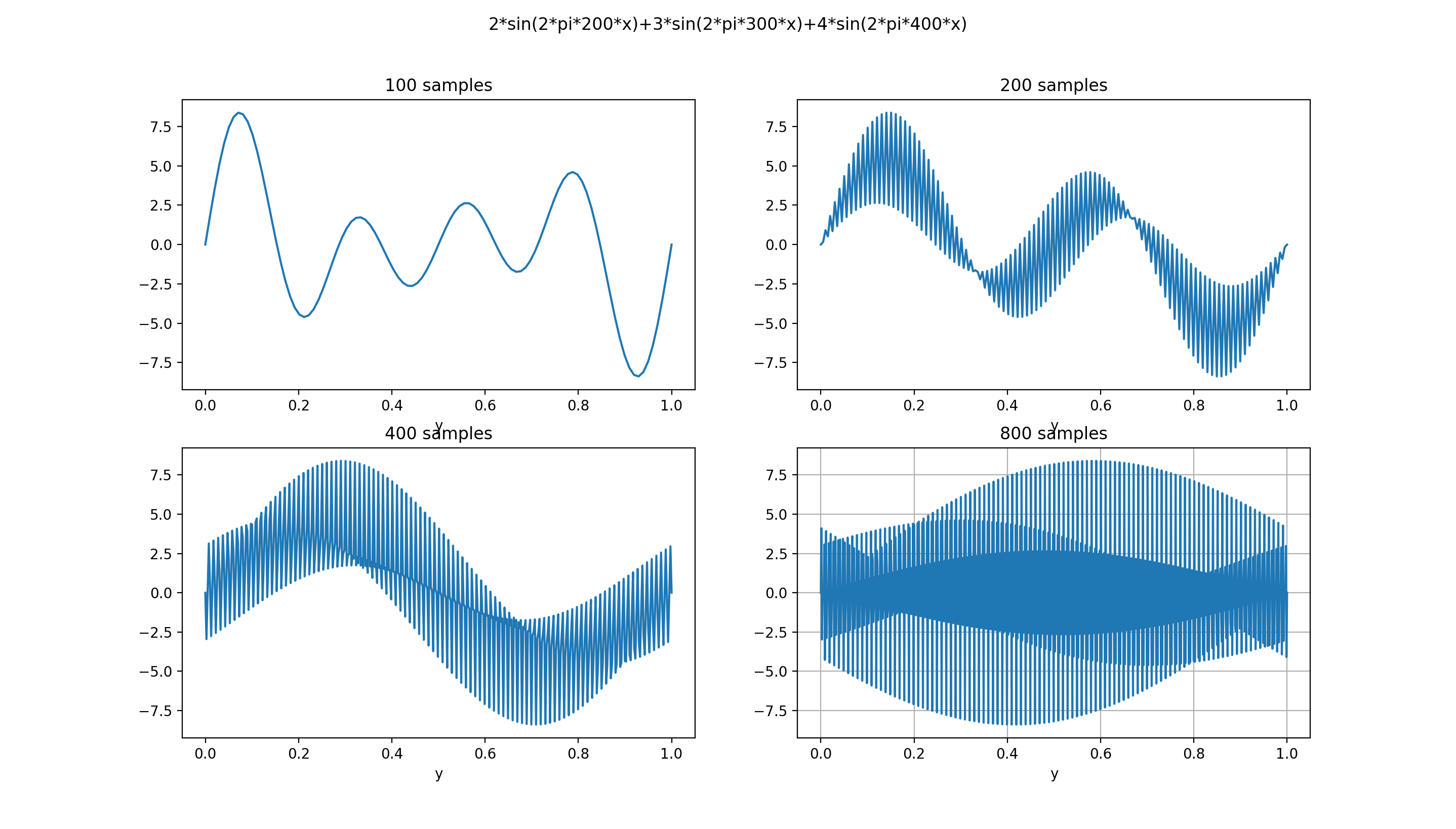
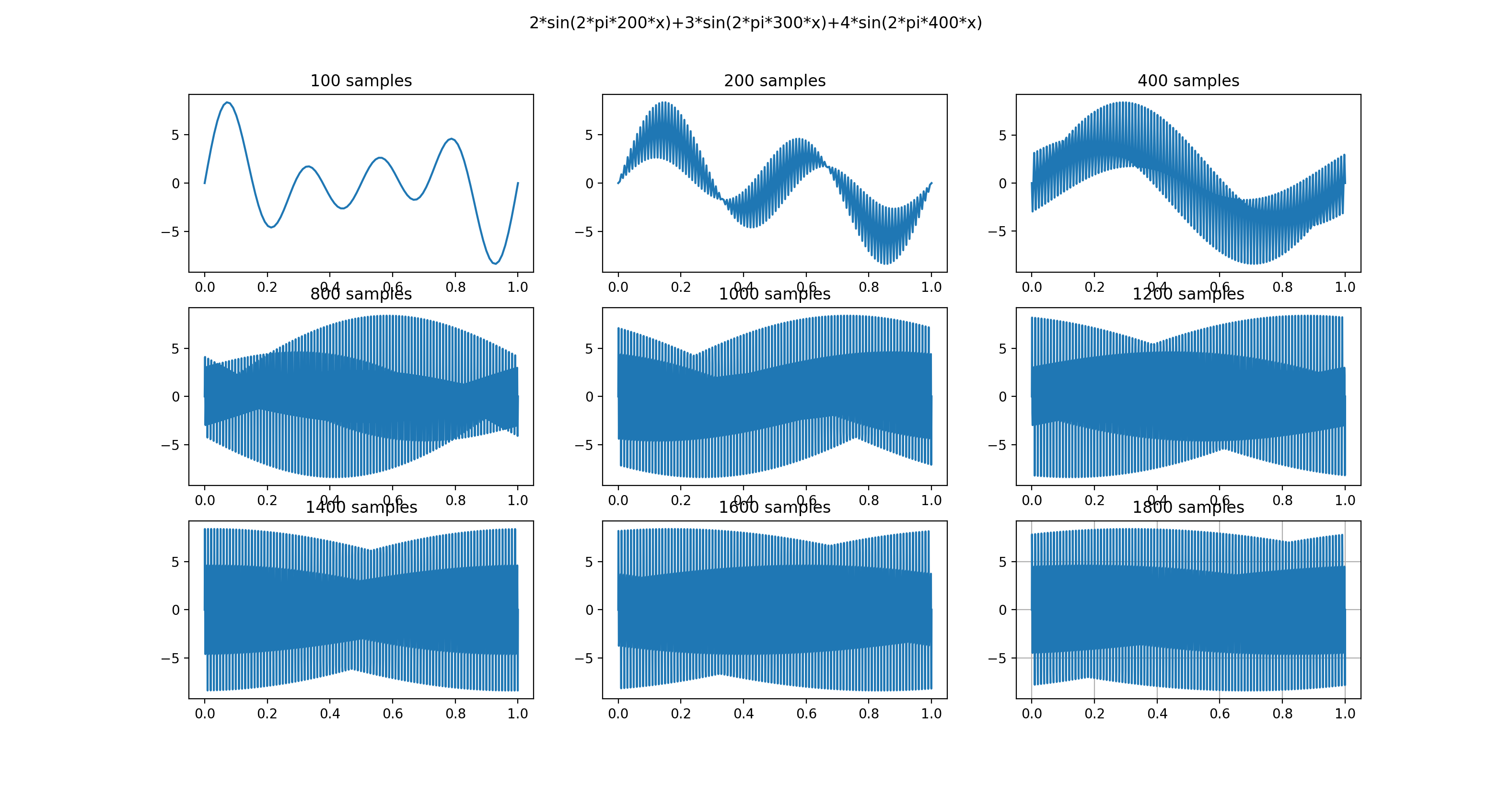
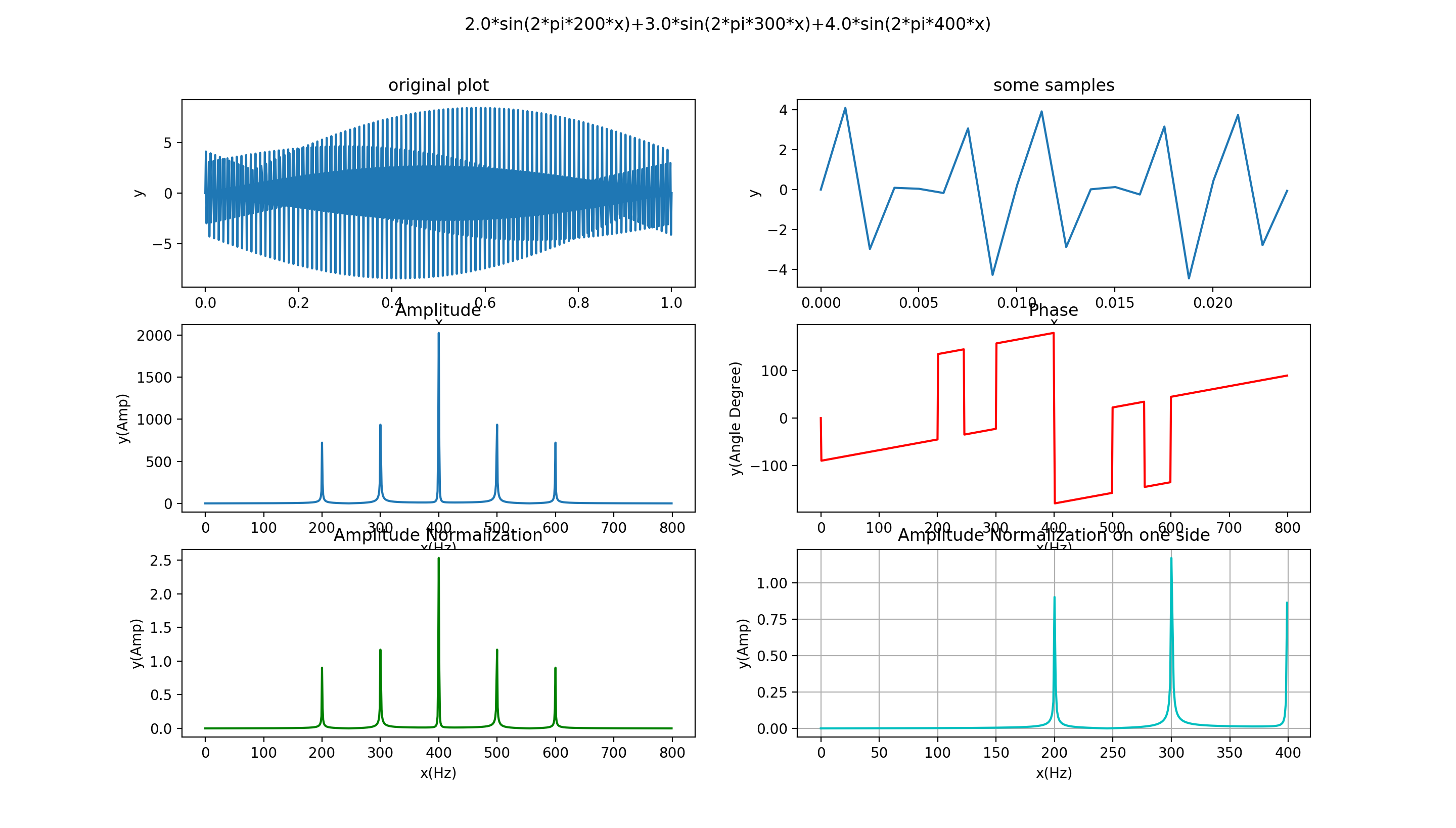
离散时间信号

在对模拟信号与系统进行时域分析时，信号用连续时间函数表示，系统则用微分方程描述；
在进行频域分析时，往往采用傅里叶变换或拉普拉斯变换方法。

Z变换在离散时间信号与LTI系统分析中扮演的作用，
正如拉普拉斯变换在连续时间信号与LTI系统分析中扮演的作用一样。

单位采样序列

单位采样序列Unit Sample Sequence，表示为$\delta(n)$，定义如下所示：

$\delta(n)=\left{\begin{array}{ll}
{1,} & {n=0} \
{0,} & {n \neq 0}
\end{array}\right.$

即单位采样序列除了在n=0处的值为1外，其他处的值均为0，也称其为单位脉冲序列。

单位阶跃序列

单位阶跃序列Unit Step Sequence，表示为$u(n)$，定义如下所示：

$u(n)=\left{\begin{array}{ll}
{1,} & {n=0} \
{0,} & {n \neq 0}
\end{array}\right.$

$u(n-m)$在n>=m时值为1，取其他值时为0。

由上图可以知道，单位采样序列和单位阶跃序列的关系为：

$\delta(n)=u(n)-u(n-1)$

$u(n)=\sum_{l=0}^{\infty} \delta(n-l)$

矩形序列

只有其中一部分为1，其他部分全部为0，如下图所示：

指数序列

指数的底数在大于1时为发散序列，小于1时为收敛序列

正弦序列

复指数序列

$x(n)=\mathrm{e}^{\mathrm{j} \omega n}=\cos (\omega n)+\mathrm{i} \sin (\omega n)$

根据欧拉公式可知，复指数序列具有以2$\pi$为周期的周期性。

周期信号

如果对所有的n，存在一个最小的正整数N，使关系式x(n)=x(n+N)成立，则称x(n)是周期为N的周期序列（Periodic Sequence），周期信号也可记为。

序列的运算

包括：

  • 加法
  • 减法
  • 移位
  • 反转
  • 尺度变换

参考

代码参考 https://www.github.com/shaoguangleo/signal_and_system

发表于 更新于 分类于 ， 阅读次数： Disqus： Valine：

离散时间系统

设系统的输入为序列x(n)，经过运算或变换得到一个输出序列y(n)，这个运算或者变换就是离散时间系统（Discrete time System）。

齐次性

若
$x(t) -> y(t)$，
则
$kx(t) -> ky(t)$

叠加性

若
$x_1(t) -> y_1(t), x_1(t) -> y_1(t)$，
则
$x_1(t) + x_2(t) -> y_1(t) + y_2(t)$

线性系统

满足叠加性和齐次性。

若
$x_1(t) -> y_1(t), x_1(t) -> y_1(t)$，
则
$k_1x_1(t) + x2(t) -> y_1(t) + y_2(t)$

时不变系统

如果系统的输出相应随输入的移位而移位，即为时不变系统。

若
$x(t) -> y(t)$，
则
$x(t-t_0) -> y(t-t_0)$

因果性

指系统的响应不应该出现在激励之前，只对自变量是时间的系统有意义。

参考

代码参考 https://www.github.com/shaoguangleo/signal_and_system

发表于 更新于 分类于 ， 阅读次数： Disqus： Valine：

信号与系统公式集锦

连续傅里叶变换 连续拉普拉斯变换（单边 ） 离散Z变换（单边） 离散傅里叶变换
时域到频域 时域到复频域 $s=\sigma + j \omega$ 离散化 $z = e^{s}$ 四种组合形式
$F(j \omega)=\int_{-\infty}^{\infty} x(t) e^{-j \omega t} d t$ $F(s)=\int_{0_{-}}^{\infty} x(t) e^{-s t} d t$ $X(z)=\sum_{n=0}^{\infty} x(n) z^{-n}$ $X(e^{jw})=\sum_{n=-\infty}^{\infty} x[n] e^{-jwn}$
$ x(t)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) e^{j w t} d \omega$ $x(t)=\frac{1}{2 \pi j} \int_{\sigma-j \infty}^{\sigma+j \infty} F(s) e^{s t} d s $ $x(n)=\frac{1}{2 \pi j} \oint X(z) z^{n-1} d z$ $x(n)=\frac{1}{2\pi} \int X(e^{jw}) e^{jwn} dw$
1 $2\pi \delta(w)$
冲激$\delta(t)$ 1
阶跃$u(t)$ $\frac{1}{s}$
$e^{jw_0t}$ $2\pi \delta(w-w_0)$
$e^{-jw_0t}$ $2\pi \delta(w+w_0)$
$e^{-at}$ $\frac{1}{s+a}$
$t^{n}$ $\frac{n!}{s^{n+1}}$
$sin(wt)$ $j\pi [\delta (w+w_0) - \delta (w-w_0)]$ $\frac{w}{s^{2}+w^{2}}$
$cos(wt)$ $\pi [\delta (w+w_0) + \delta (w-w_0)]$ $\frac{s}{s^{2}+w^{2}}$
$e^{-at}sin(wt)$ $\frac{w}{(s+a)^{2}+w^{2}}$
$e^{-at}cos(wt)$ $\frac{s+a}{(s+a)^{2}+w^{2}}$
$te^{-at}$ $\frac{1}{(s+a)^{2}}$
$t^{n}e^{-at}$ $\frac{n!}{(s+a)^{n+1}}$
$tsin(wt)$ $\frac{2ws}{(s^{2}+w^{2})^2}$
$tsin(wt)$ $\frac{s^2-w^2}{(s^{2}+w^{2})^2}$
时域卷积$f(t)\ast g(t)$ $F(w) \times G(w)$
时域乘积$f(t)\times g(t)$ $\frac{1}{2\pi}F(w) \times G(w)$

性质

性质 时域 傅里叶变换
对称性 $F(t)$ $2\pi f(-w)$

傅里叶变换的四种表示形式

参考

代码参考 https://www.github.com/shaoguangleo/signal_and_system

发表于 更新于 分类于 ， 阅读次数： Disqus： Valine：

信号的频谱分析

正交函数集合

傅里叶级数

傅里叶变换

傅里叶变换：

$F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-j \omega t} d t$

傅里叶反变换：

$f(t)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) e^{j \omega t} d \omega$

交换存在的条件：

  • 绝对可积
  • 极值点有有限个
  • 间断点有限

典型信号的傅里叶变换

傅里叶变换的性质

周期信号的傅里叶变换

参考

代码参考 https://www.github.com/shaoguangleo/signal_and_system

发表于 更新于 分类于 ， 阅读次数： Disqus： Valine：

LTI系统时域分析

  • 用脉冲表示离散时间信号
  • 离散时间LTI系统对单位脉冲$\delta[n]$的响应$h(n)$称为离散时间LTI系统的单位脉冲响应。

时间阈分析方法直接分析时间变量的函数，研究系统的时间相应特性，或者成为时域特性。

系统分析的一般过程：

通过实际物理系统或者系统框图构建模型，求解该模型，并进行分析。

方程求解

经典求解

  • 微分方程 $\sum_{k=0}^{N} a_{k} \frac{\mathrm{d}^{k} y(t)}{\mathrm{d} t^{k}}=\sum_{k=0}^{M} b_{k} \frac{\mathrm{d}^{k} x(t)}{\mathrm{d} t^{k}}$
    • 电路系统
    • 力学系统
    • 系统框图
  • 差分方程 $\sum_{k=0}^{N} a_{k} y[n-k]=\sum_{k=0}^{M} b_{k} x[n-k]$
    • 微分方程离散化
    • 物理系统建立
    • 系统框图建立

解的分析

  • 自由(齐次解，反映系统本身的特性)、强迫（特解，对输入信号的反应）
  • 稳态（时间无限大时，保留下来的部分）、瞬态（时间无限大时，趋于0的部分）
  • 零状态、零输入
    • 零状态：系统在起始条件为零的情况下的系统对于输出信号的输出响应
    • 零输入：系统在没有外部输入信号的情况下，由内部起始条件所产生的响应

卷积和卷积和

使用卷积的前提，系统为LTI，并且为零状态响应。

这里还设计到相关的概念，如果是复数，为第二个函数的共轭，所以不具备交换律。

特性

  • 交换律
  • 分配律
  • 结合律
  • 积分 $\int_{-\infty}^{t}[x(\tau) * h(\tau)] \mathrm{d} \tau=x(t) * \int_{-\infty}^{t} h(\tau) \mathrm{d} \tau=\left[\int_{-\infty}^{t} x(\tau) \mathrm{d} \tau\right] * h(t)$
  • 微分 $\frac{\mathrm{d}}{\mathrm{d} t}[x(t) * h(t)]=x(t) * \frac{\mathrm{d}}{\mathrm{d} t} h(t)=\frac{\mathrm{d}}{\mathrm{d} t} x(t) * h(t)$
  • 延时计算 若$x(t) * h(t) = y(t)$， 则$x(t-t_1) * h(t-t_2) = y(t-t_1-t_2)$

应用

滤波

信号中的噪声往往造成信号在真实值附近的快速拨动，可以通过对该时刻附近的取值进行加权平均达到去噪的目的。
这个过程可以看做将信号与平滑滤波函数的卷积过程。

参考

代码参考 https://www.github.com/shaoguangleo/signal_and_system

发表于 更新于 分类于 ， 阅读次数： Disqus： Valine：

信号的分类

确定性信号 与 随机信号

按照函数值的确定性。

  • 确定性信号：在任意时刻都有确定的取值 （一般为人工设计）
  • 随机信号：每一刻取值都为随机

连续时间信号 与 离散时间信号

按照信号按照时间是否连续。

  • 连续时间函数 ： 随时间联系
  • 离散时间函数 ： 只有某些时间点有值

按照自变量和函数取值的情况，分为：

  • 模拟信号：信号的自变量和函数值的幅值连续
  • 离散时间信号：信号只能在规定的离散点取值，自变量的取值离散，而函数值是连续的
  • 数字信号：函数值和自变量的幅值均离散

模拟信号的数字处理方法就是将待处理的模拟信号经过采样、量化和编码形成数字信号。

能量信号 与 功率信号

根据能量的特性。

  • 连续功率信号 $P=\lim {T \rightarrow \infty} \frac{1}{T} \int{-\frac{T}{2}}^{-\frac{1}{2}}|f(t)|^{2} d t$
  • 连续能力信号 $E=\int_{-\infty}^{\infty}|f(t)|^{2} d t$
  • 离散功率信号 $P=\lim {n \rightarrow \infty} \frac{1}{2 N+1} \sum{n=-N}^{N}|x[n]|^{2}$
  • 离散能量信号 $E=\sum_{n=\infty}^{\infty}|x[n]|^{2}$

周期信号 与 非周期信号

确定信号按照函数值的重复性来区分。

$f(t)=f(t+\delta t)$

周期信号的复合可能是周期信号也可能是非周期信号。

参考

代码参考 https://www.github.com/shaoguangleo/signal_and_system

发表于 更新于 分类于 ， 阅读次数： Disqus： Valine：

系统的分类

连续时间系统 与 离散时间系统

  • 连续时间系统：输入、输出、系统内部信号都是模拟信号
  • 离散时间系统：输入、输出信号都是序列的系统

按照输入输出信号的类型，分为：

  • 模拟系统
  • 离散时间系统
  • 数字系统

即时系统 与 动态系统

根据有没有储能元件来区分

  • 即时系统：无记忆系统，系统的输出只与当时时刻的输入有关，与其他时刻的输入无关，用代数方程描述
  • 动态系统：记忆系统，系统的输出不只与当前时刻的输入有关，用微分方程或者差分方程描述

线性系统 与 非线性系统

如果一个系统既满足叠加性也满足齐次性就称为线性系统，否则为非线性系统。

时变系统 与 时不变系统

如果一个系统当输入信号有一个时移时，输出相应也有一个对应的时移，信号的波形并不发生变化为时不变系统。
反之即为时变系统。

可逆系统 与 不可逆系统

如果一个系统对任何不同的输入都能产生不同的输出，即输入与输出是一一对应的关系，这称为可逆系统，
否则为不可逆系统。

因果系统 与 非因果系统

如果一个系统的任何时刻的输出只与当时这个时刻的输入以及以前的输入有关，而和该时刻以后的输入无关，称为因果系统，
否则为非因果系统。

稳定系统 与 非稳定系统

  • 稳定系统：BIBO（Bound Input Bound Output）及输入有界时，产生的输出也是有界的，反之为非稳定系统

参考

代码参考 https://www.github.com/shaoguangleo/signal_and_system

发表于 更新于 分类于 ， 阅读次数： Disqus： Valine：

信号的表示方法

信号是带有信息（比如语言、音乐、图像、数据等等）的随着时间（和空间）变换的物理量或者物理现象，其图像称为信号的波形。

信号的时间特性即为信号随着信号变化快慢的特性，体现为信号的周期和信号中单个脉冲的持续时间及上升时间和下降时间的不同。

信号有四种方法的表现形式，如下所示：

  • 函数
  • 图形、波形
  • 变换域表示
  • 分配函数

举个例子如下，比如函数的形式为(包含三个频率，分别为200，300和400Hz)：

$y = 2 \times sin(2\times\pi \times 200 \times x) + 3 \times sin(2\times\pi \times 300 \times x) + 4 \times sin(2\times\pi \times 400 \times x) $

而图形的形式如下，在我们从0到1进行100个采样点的时候，如下：

多进行一些采样设置，如下图：

可知在不同的采样率上，展示的图形也是不同的。
这里的主要原因为按照奈奎斯特采样定理，采样点数至少为400Hz的2倍，即800Hz，即在1s内采样800个点，我们再来绘制一幅图，采样更多的点数。

由图可知，在采样点数超过800后，采样的图形基本一致，所以低于800点的采样其实无法还原原始函数或者图形的。

频域表示

信号的频率特性可以由频谱来描述。

比如有一个信号如下：

$Y=A1+A2cos(2\piω2+φ2）+A3cos(2\piω3+φ3）+A4*cos(2\piω4+φ4）$

经过FFT之后，得到的“振幅图”中，

第一个峰值（频率位置）的模是A1的N倍，N为采样点，

第二个峰值（频率位置）的模是A2的N/2倍，N为采样点，

第三个峰值（频率位置）的模是A3的N/2倍，N为采样点，

第四个峰值（频率位置）的模是A4的N/2倍，N为采样点，

依次下去……

进行归一化处理，既然第一个峰值是A1的N倍，那么将每一个振幅值都除以N即可

FFT具有对称性，一般只需要用N的一半，前半部分即可。

其实fft都是离散的一些点，如果不使用连线，可以得到如下图像：

参考

代码参考 https://www.github.com/shaoguangleo/signal_and_system