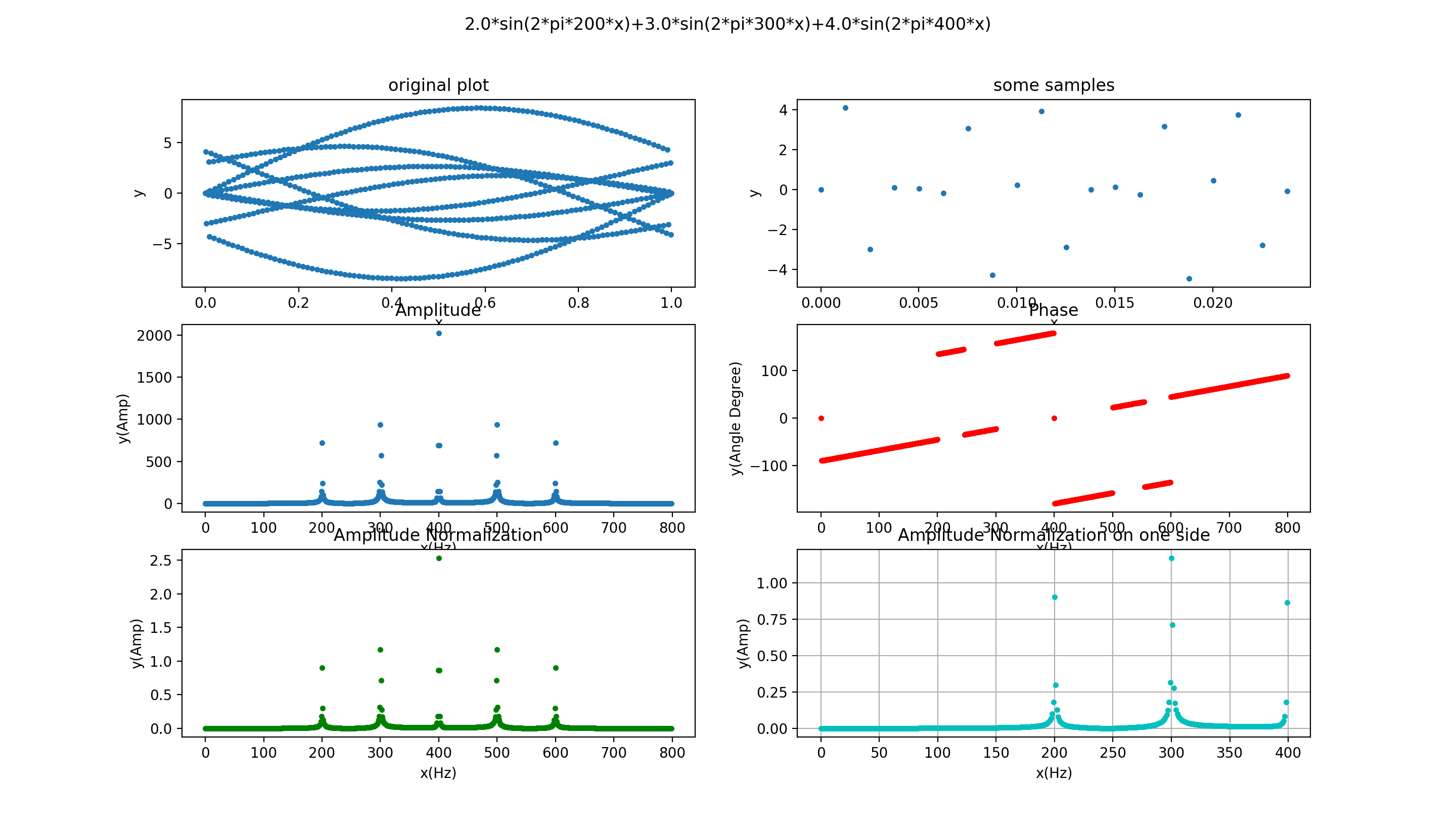
信号的表示方法

信号是带有信息（比如语言、音乐、图像、数据等等）的随着时间（和空间）变换的物理量或者物理现象，其图像称为信号的波形。

信号的时间特性即为信号随着信号变化快慢的特性，体现为信号的周期和信号中单个脉冲的持续时间及上升时间和下降时间的不同。

信号有四种方法的表现形式，如下所示：

举个例子如下，比如函数的形式为(包含三个频率，分别为200，300和400Hz)：

$y = 2 \times sin(2\times\pi \times 200 \times x) + 3 \times sin(2\times\pi \times 300 \times x) + 4 \times sin(2\times\pi \times 400 \times x) $

而图形的形式如下，在我们从0到1进行100个采样点的时候，如下：

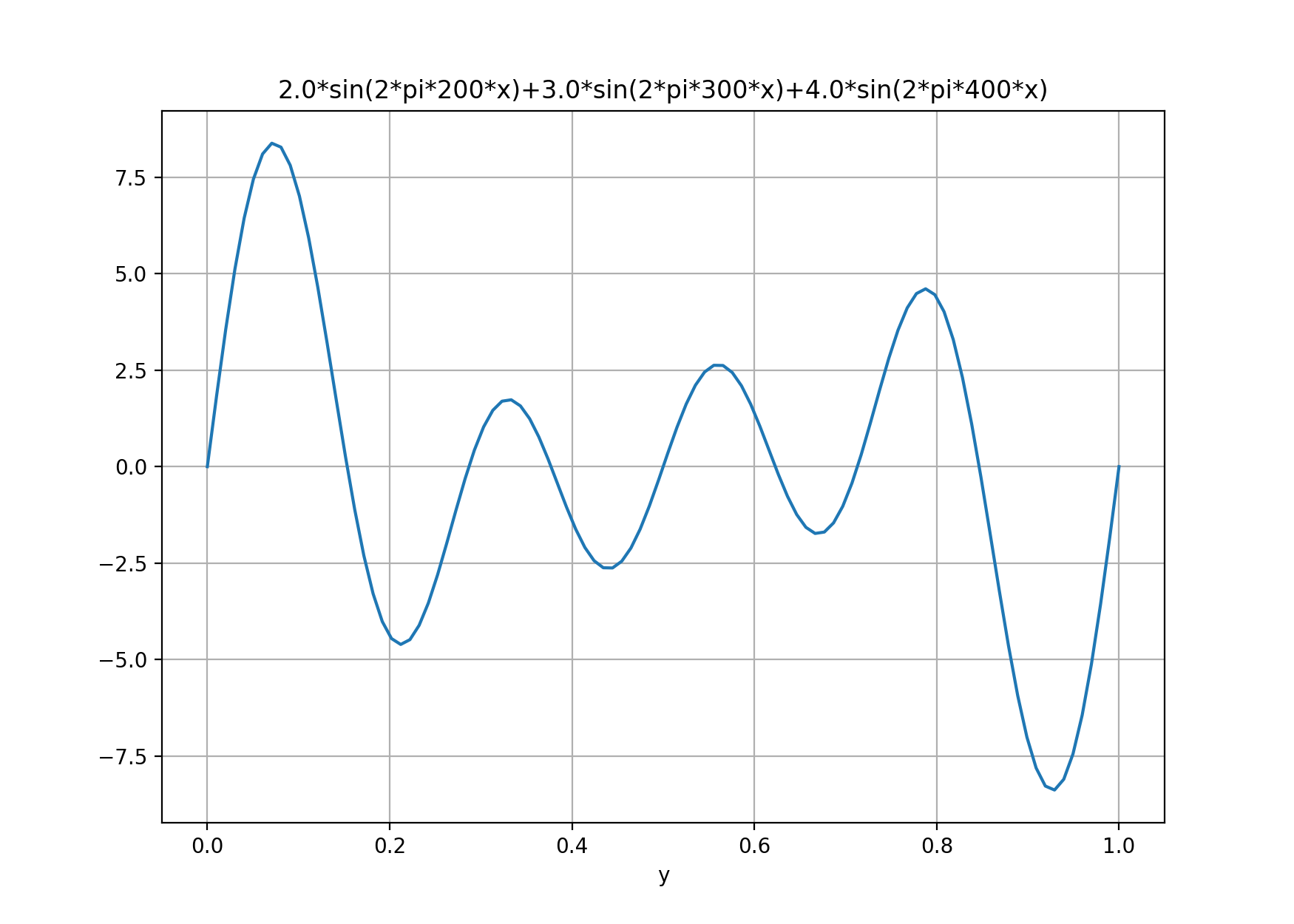
多进行一些采样设置，如下图：

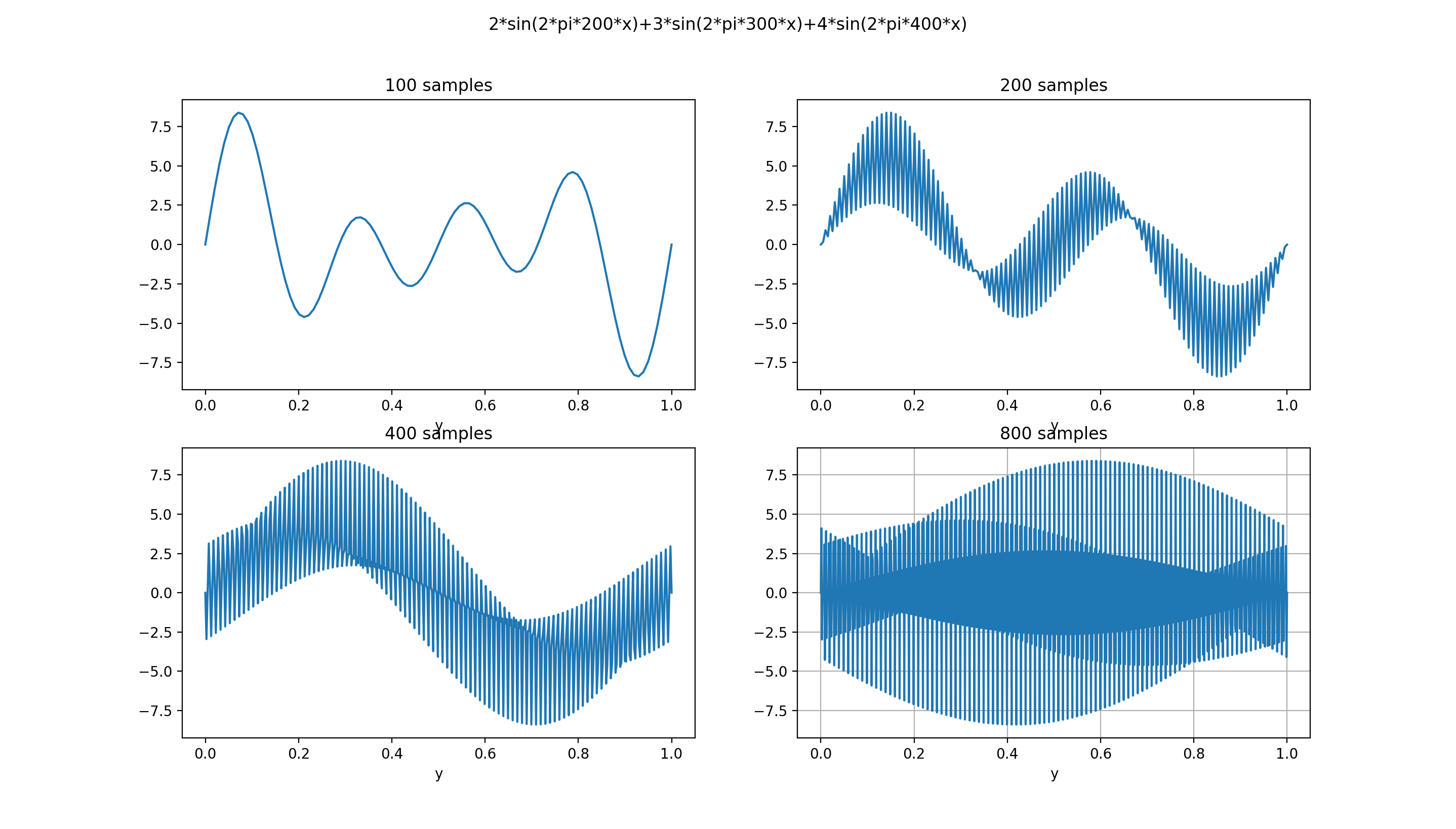
可知在不同的采样率上，展示的图形也是不同的。
这里的主要原因为按照奈奎斯特采样定理，采样点数至少为400Hz的2倍，即800Hz，即在1s内采样800个点，我们再来绘制一幅图，采样更多的点数。

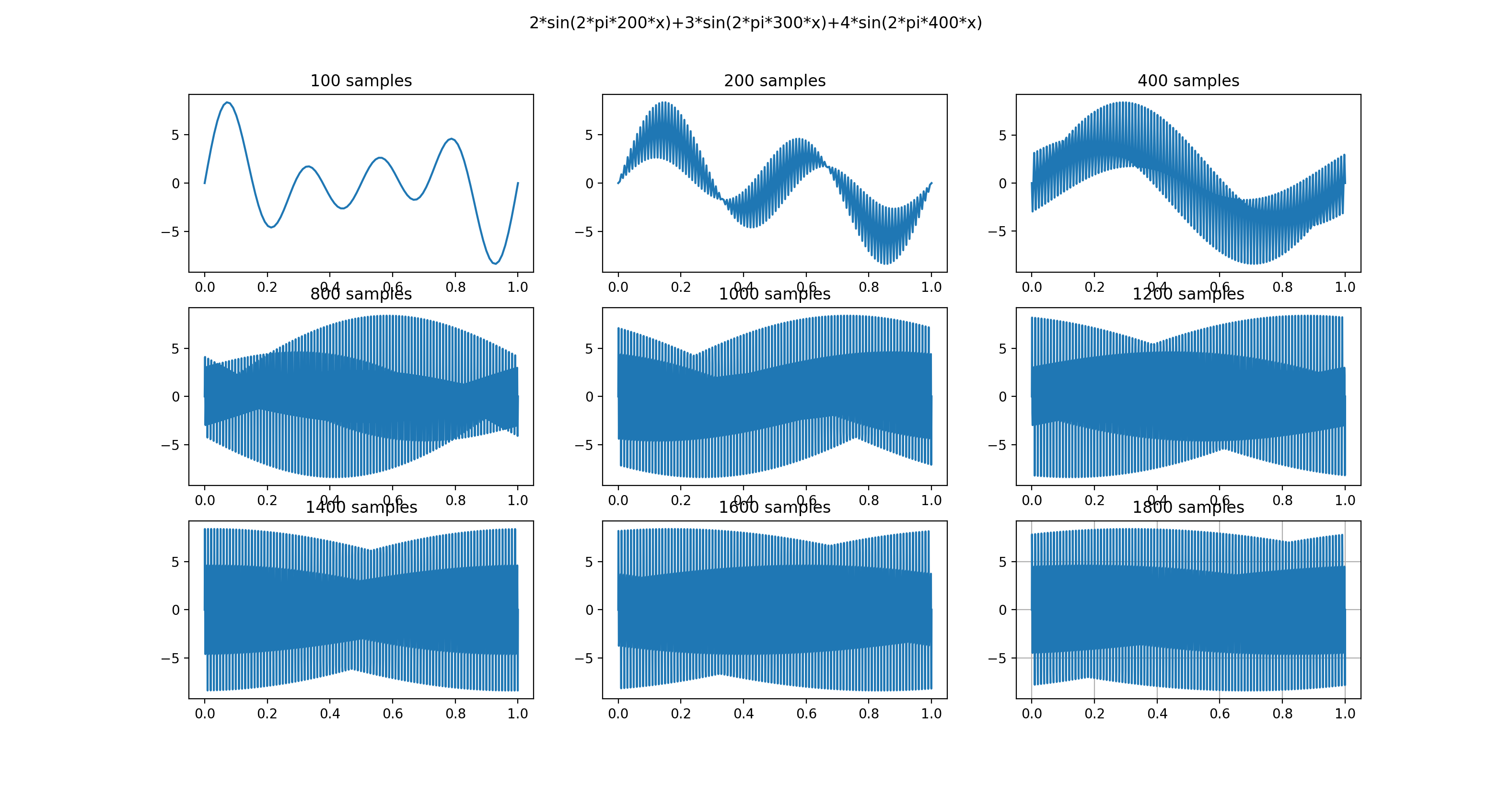
由图可知，在采样点数超过800后，采样的图形基本一致，所以低于800点的采样其实无法还原原始函数或者图形的。

频域表示

信号的频率特性可以由频谱来描述。

比如有一个信号如下：

$Y=A1+A2cos(2\piω2+φ2）+A3cos(2\piω3+φ3）+A4*cos(2\piω4+φ4）$

经过FFT之后，得到的“振幅图”中，

第一个峰值（频率位置）的模是A1的N倍，N为采样点，

第二个峰值（频率位置）的模是A2的N/2倍，N为采样点，

第三个峰值（频率位置）的模是A3的N/2倍，N为采样点，

第四个峰值（频率位置）的模是A4的N/2倍，N为采样点，

依次下去……

进行归一化处理，既然第一个峰值是A1的N倍，那么将每一个振幅值都除以N即可

FFT具有对称性，一般只需要用N的一半，前半部分即可。

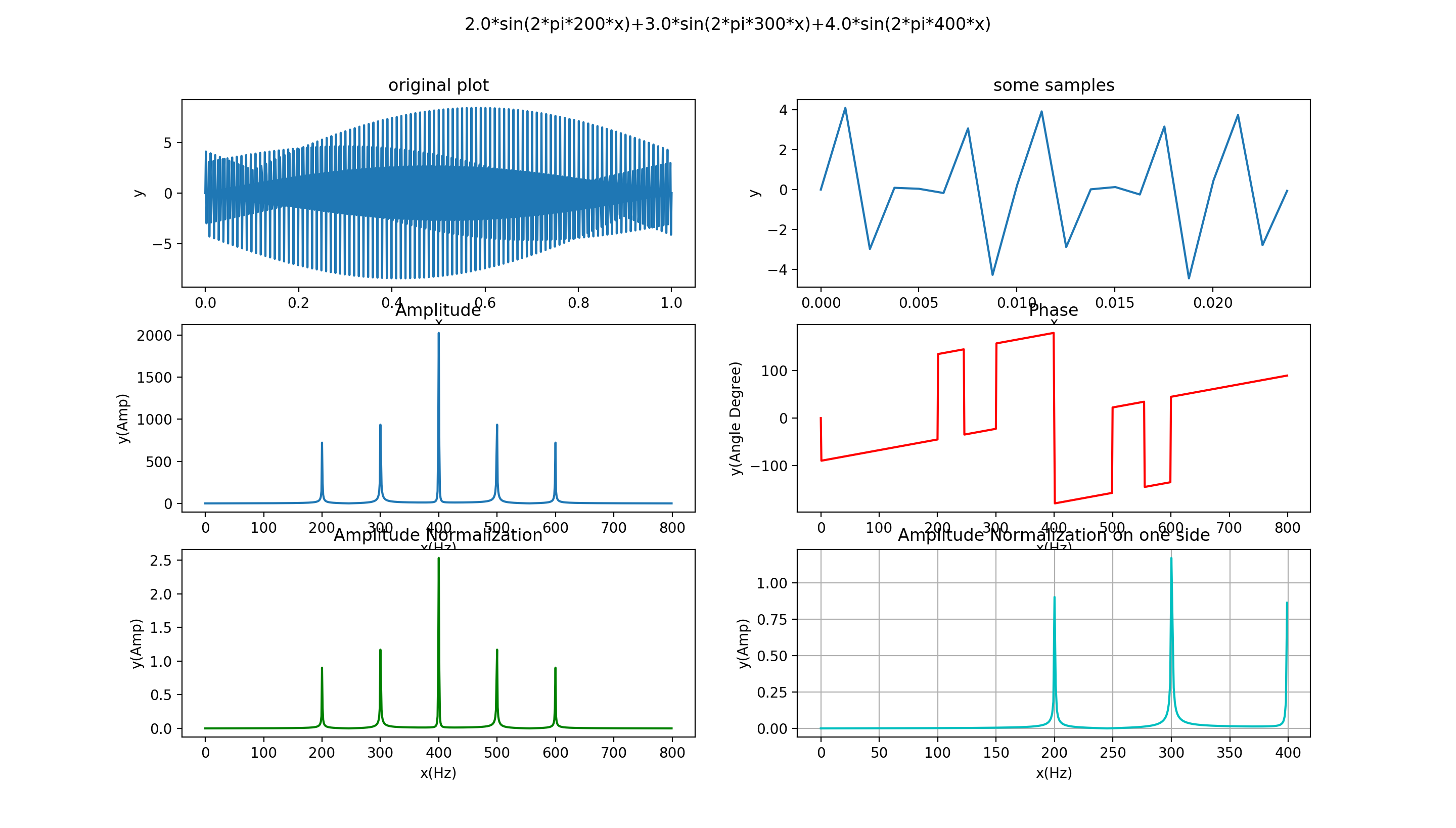
其实fft都是离散的一些点，如果不使用连线，可以得到如下图像：